The phenomena of inertia and friction at the level of the boundary layer must be explained briefly to better understand what is happening at the level of the rail.
Fluids in motion, in contact with walls, follow the shape of the surface because to move away from it would create areas of voids and low pressures which immediately reattach the particles to the wall. The fluid zone thus “sucked up” by the wall is called the boundary layer.
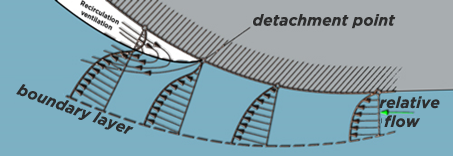
When the speed difference becomes significant, between the braked particles in direct contact with the wall, and the more distant particles, a proportional pressure difference is produced (see Bernoulli). The overpressure causes the detachment of the particles in contact with the wall. See (Rebuffet). The detached particles then follow the general flow of the fluid away from the wall and the void zone is filled by recirculations of water, or air if the wall is close to the surface. This point of recirculation and separation of the boundary layer is also influenced by the curve of the surface and the inertia of the fluid. The position of this point therefore evolves according to the speed and the radius of curvature of the surface. Sailing enthusiasts observe this phenomenon well when trimming their sail, by monitoring the marker filaments (telltales) on the upper surface: When the telltales reverse, they highlight the phenomenon of recirculation and indicate to the sailor that the curve canvas is too strong. If the wind speed is high, the angle of deviation that it accepts without stalling is small, so the sail must be flattened and taut. If the wind is light, it has little inertia and can withstand tacking without stalling, the sail curvature may be significant.
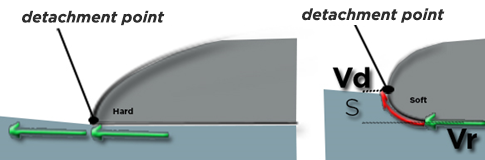
By choosing the radius of curvature of the rail, it is possible to control the position of the separation and impose a change of direction on the fluid, or else let it continue on its way without modifying its trajectory. The absence of a radius of curvature (hard rail) forces the detachment, the fluid does not modify its trajectory, no force is transmitted to the board. A wide radius of curvature (soft rail), brings the detachment point and out of the trajectory, generating a deflection of the liquid mass, exerting a reaction force on the board.
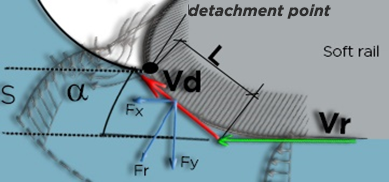
These formulas make it possible to evaluate the forces that the shape of the rail can produce:
Fx = Qm x (Vr -Vr x cos (α)) Equation 55
Fy = Qm x Vr x sin (α) Equation 56
ake for example a soft rail in a relative flow of 20 km/h (5.5m/sec). Suppose also that the planing angle is zero to analyze only the impact of the rail on the flow. Let’s evaluate the rail effects over an element width of 0.3m. Let's estimate that this soft rail has a point of separation at 0.02 m from the bottom (length L in the diagram) and calculate the forces for angles α from 10° to 40°. 40° being the maximum angle that can be applied without separation, above this angle, the flow will not follow the curve and one can consider the flow, stalled as on a hard rail, therefore without force of rail suction. Note that the detachment can be caused by a lack of roughness, or a mark on the surface. The sanding of the junction of the bridge and bottom glazings must therefore be careful at the level of the rail to avoid triggering an unwanted detachment.
Note that the point of separation modifies the wetted length of the element, therefore the total planing surface. We consider here this variation as negligible and estimate the detachment position in a very approximate way, we propose later a method of calculating this position of detachment point, but for the moment this approach is enough for us to evaluate the impact of the rail .
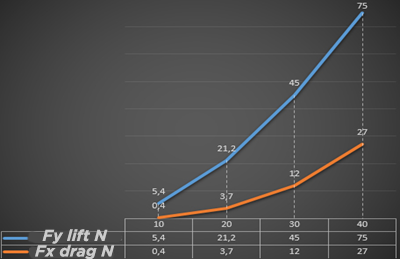
This graph shows that an area of soft rail 0.3m wide, with a lift angle of 40° can produce a maximum suction Fy, of approximately 7.5kg (75N) helping the rider to immerse their rail in the wave. An Fx component of about 3 kg (27N) is added, it produces a suction from the nose of the board towards the inside of the wave, helping the surfer to tackle in the verticality of the Still point. Note that the lift/drag ratio is greater at low take-off angles.