Experienced surfers or beginners, surf school teacher or shaper, we all have an interest in understanding what conditions must be met for a take off to be possible: What interests us here is the aspect surfing physics, and more particularly: The take off. Wwe will therefore not detail here the pedagogy of the take off, a search for "learn take off surf" on the net gives very good lessons on this subject. From the surfer's point of view, the take off is the moment when he stands up on his board, to take control of his trajectory in a standing position. But getting up on the board is not enough, it has to be done in the right place and at the right time.

The more experienced the surfer, the more he masters a series of repeated gestures that turn into a reflex. This instinct, reinforced by experience, encompasses without distinguishing between them the various specific conditions necessary for the take off, like a sensation, allowing this take off. We think: this will do it, and Action! If it does the job , great! Why dig deeper?
But If that doesn't do the job?, or if the surfer wants to improve his take off?, or simply explain to the shaper what should be improved on the board? It then becomes useful to dig a little, under the instinct, to find understandable and shareable arguments. We will therefore define here the take off, not as an action of the surfer, but as the sum of the conditions making it possible. Because it is by describing and understanding each of these necessary conditions that we can improve our take-off, or the board.
The numerical arguments are provided here for the sake of transparency, but the reader can easily skim over the formulas that he finds off-putting, and simply take note of the conclusions that will be useful to him in his search for optimization of his take off or his board.
The 3 take off conditions:
- Speed: No choice, this parameter depends on the wave! Catching a wave is catching the bandwagon! The surfer must reach the crest speed imposed by the wave: If the surfer is moving at a speed lower than that of the wave, when the crest reaches his level, he will be overtaken by the wave. This is obvious, but we will see later that obtaining this speed is a strategy, skilfully developed by the shaper, depending on the surfer and the wave.

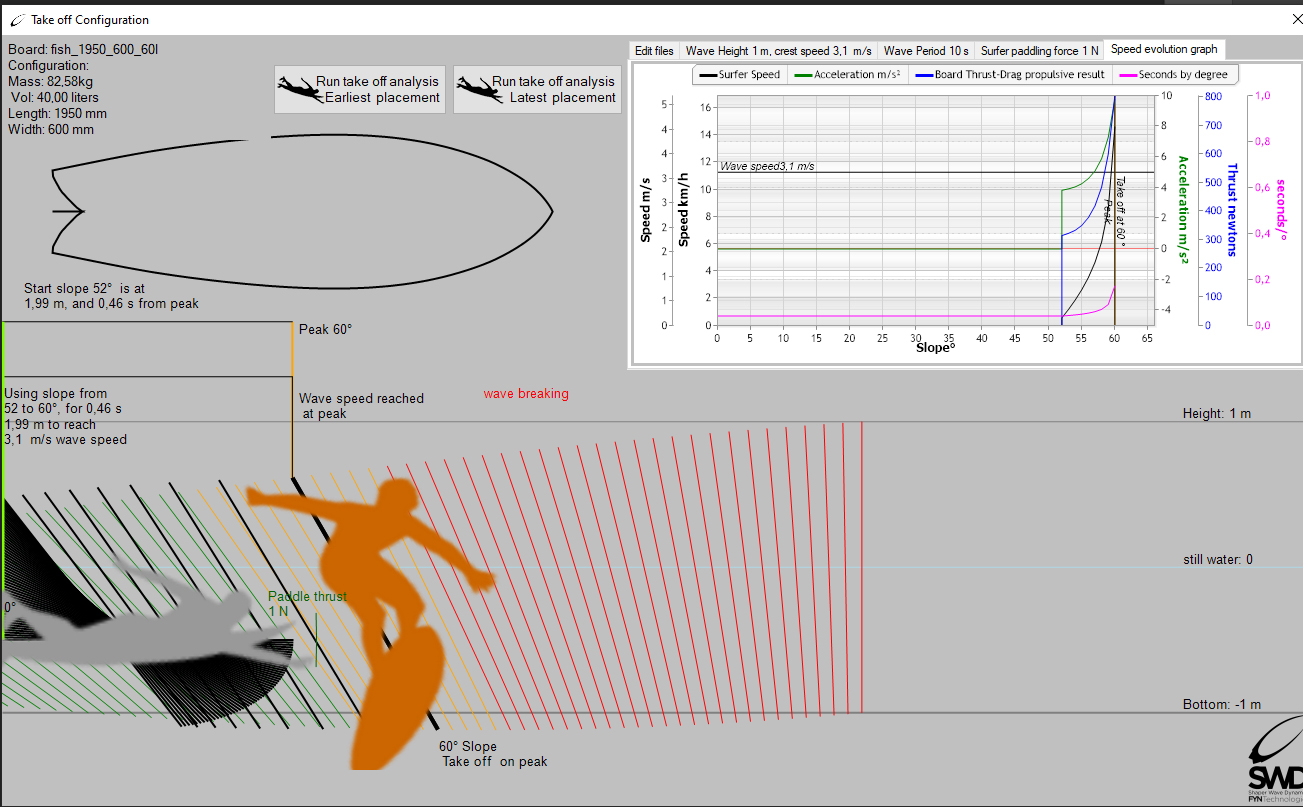
- The placement: The placement of the surfer is relative to the peak. The surfer must identify where the peak will appear by observing the wave, and be able to point it out with their finger well before it breaks. It is a fixed geographical point, the surfer can use land markers (see "navigation alignments"). But the position of the peak is only a benchmark, waiting for the wave at the peak is a very bad idea! When the peak arrives, the surfer must already have acquired the speed of the wave, and have already performed his take off. For a surfer alone on the spot, the placement consists of estimating the rowing distance necessary to reach the top speed, before the peak is reached. the surfer will therefore have to position himself outside the peak, at a distance slightly greater than the speed pick-up distance. We will come back in detail to the different strategies available to the surfer to choose the necessary distance.
(Interface detail Analysis take off, of the software ShaperWaveDynamics)
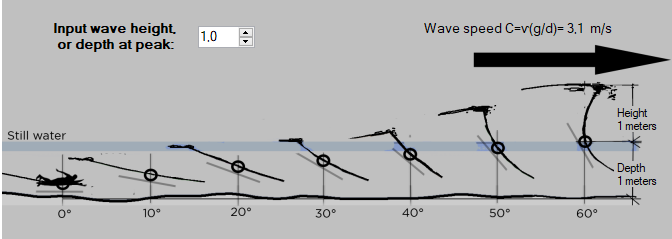
- The moment: the slope of the take off: LThe moment of the take off is also relative to the peak. Let's assume for our purposes that the breaking of the peak begins when the wave face reaches a maximum slope of around 60 degrees. The surfer must therefore have reached the peak speed, before the slope reaches 60 degrees. The moment of the take off must be as far ahead as possible of this moment when the slope crosses 60 degrees. If the surfer recovers after 60 degrees, the (late) take off will be very technical or even impossible, on the other hand, if the take off is made before 60 degrees, the surfer will be able to choose his trajectory with more freedom. Note that we take care here to replace the notion of time, by the geometric notion of slope. (see geometric surf thought) We can say that, the lower the slope at the time of the take off, the more space and choice the surfer will have to adjust his trajectory before the break (60°). The shaper will note that a board will provide more freedom and ease if it promotes low slope take off. The shaper has a great interest in controlling this parameter, which we will therefore detail later. But let's see another essential point that connects the period and the variation of the slope:
:
(Interface detail Analysis take off, of the software ShaperWaveDynamics)
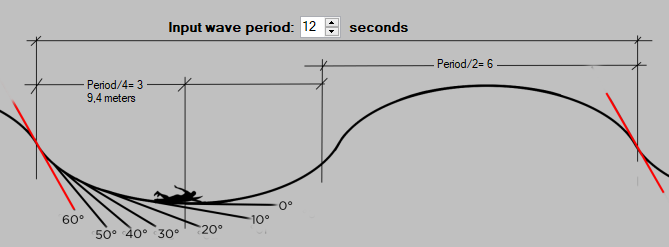
The slope of a wave varies according to a cycle of one period (take for example 12 seconds), it therefore passes from a slope of zero in the low position, to a slope of zero in the high position, during 1/2 period ( 6 s), and we can estimate that it goes from zero to 60 degrees, in the rising phase in 1/4 of a period (3 s). This estimate is largely precise enough for the subject that interests us: We can estimate that a surfer, positioned at the peak without moving, sees the wave go from 0 to 60 degrees in 1/4 of a period (3s). It is in fact the time during which the surfer will be exposed to a propulsive component of the slope, if he does not move. We will simply note here that the surfer is exposed to the propelling slope for less time in a wave of short period than in a wave of long period, we will see later what this implies......
To sum up, the 3 minimum "limit" conditions of the take off are:
- Sufer speed = peak speed. when the surfer reaches the peak speed, he realizes the take off.
- Surfer Placement =Distance required to reach peak speed. If the peak speed is reached before the peak, it is an advantage for the surfer
- The slope at take off=Before 60 degree slope. The lower the take-off slope, the more freedom and advance surferhas on the wave and any competitors.. But let's note a limit to this: the concept of minimum propulsive slope: The board is subjected to a drag force, which opposes and diminishes the "useful" propulsive force. The useful propulsive force, Fpu, is thus: Fpu= Fp-drag. If Fpu<0, the board slows down. When the surfer is no longer rowing, the force of propulsion, Fp, is produced only by the slope. It is therefore premature to take-off on a slope that does not produce a useful propulsive force>0.We will name Minimum propulsive slope, the slope which produces a propulsive force greater than the drag, therefore a useful propulsive force greater than zero, for a surfer and a given board, at a given speed. The ideal take-off slope, in terms of advance on the surge, and any competitors, will never be less than the minimum slope, but as close as possible.
Let's now go over these conditions in detail and see what they imply:
The speed condition:
- The speed of the wave (in shallow water) is given by the formula C= sqrt(9.81/Depth). This implies that a wave breaking on a bottom of 3 meters is faster than a wave breaking on a bottom of 1 meter. Remember that the speed of the wave depends solely and simply on the depth at the peak, and that we have no leverage to modify this fact. We have to produce this speed somehow, otherwise no wave!
- Acceleration: Reaching speed means increasing the surfer's speed from zero to peak speed. This is formulated in physics, by the notion of Acceleration: a=(Vc-V0)/dt, with a = acceleration in m/s², V0=initial speed m/s, Vc = peak speed m/s, and dt = time interval in seconds, during which the speed goes from v0 aVc. Example: To go from 0 to 3.1 m/s in one second (speed of a wave of 1m), consists in accelerating from a= (3.1-0)/1= 3.1 m/s². If you have 2 seconds to perform this speed variation, the acceleration is even lower: A= (3.1-0)/2= 1.55 m/s². Note that the more time we have to reach a given speed, the less we need to accelerate..
- Propellant source: To obtain the speed, the surfer therefore uses a propulsive force, Fp, which can come from various sources:
- Rowing muscular strength: A powerful surfer produces around 140 newtons (very variable value depending on the surfer and his condition)
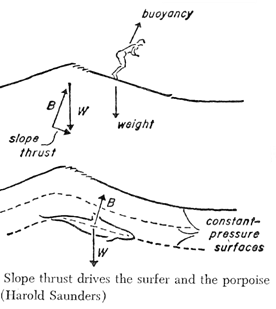
- Projection of the lift of the board: this result depends on the slope and the weight of the surfer
- sail traction, jet ski, engine + propeller....
Fp= sum of propulsive forces
- Propulsive resistance: the board is unfortunately subject to a drag force, which opposes and diminishes the force of propulsion. This hydrodynamic drag force evolves according to the square of the speed, and strongly depends on the weight, the incidence and the shape of the board. We will come back to it, and will simply remember here that the hydrodynamic drag reduces the propulsive force.
- Useful propulsion force: the board is therefore subjected to a force of resistance to progress, called drag, which opposes and reduces the "useful" propulsion force. The useful propulsion force, Fpu, is therefore :
Fpu= Fp-Drag.
This useful propelling force provides the acceleration described by Newton's law: Fpu=m*a. We can thus estimate the force necessary to accelerate a surfer of a given weight..
example: To propel an 80 kg surfer, stationary at a peak speed of 3.1 m/s (wave 1 meter), a force Fpu must be applied, of: Fpu=m*a=>Fpu=80*( 3.1-0)/1=248 newtons (approximately 25 kgf). As we saw above, if we have 2 seconds to perform this acceleration, the force is reduced by 2: Fpu=80*(3.1-0)/2=124 newtons (approximately 12.5 kgf). We will retain a very important point for the strategy of the take off: the more time we have for picking up speed, the less force we need!
To sum up, the speed, imposed by the wave, therefore imposes the acceleration. The weight of the surfer and the wave speed, being factors over which the surfer has no power at the time of the take off, the 2 levers remaining at his disposal to acquire the wave speed, are the acceleration time and the propulsive force.
At this stage we must agree on the definition of the propulsive force: As we have seen above, the propulsive force is thwarted by a force of resistance to progress: the hydrodynamic drag:
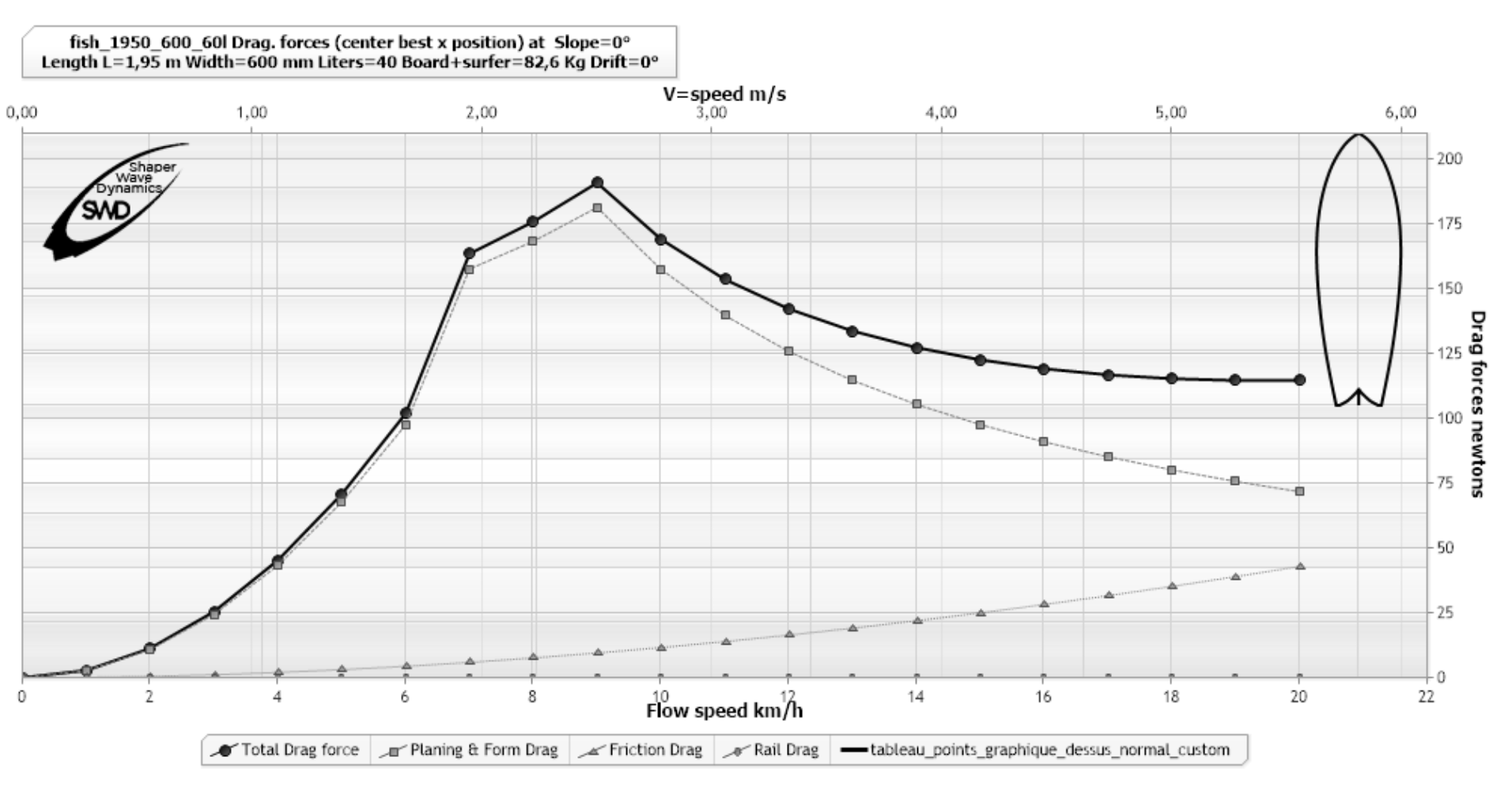
(example Hydrodynamic drag analysis, software ShaperWaveDynamics)
The curve (black round dots) of this graph shows the hydrodynamic drag variation of a given board with a given surfer, in a range of 0 to 22 km/h. This graph shows, for example, that the drag of the board at 4 km/h is around 45 N. It is the force that must be provided to maintain speed. If we apply a greater force, we accelerate, if we apply a lower force, we decelerate, if the propulsive force is equal to the drag force, the speed is constant..
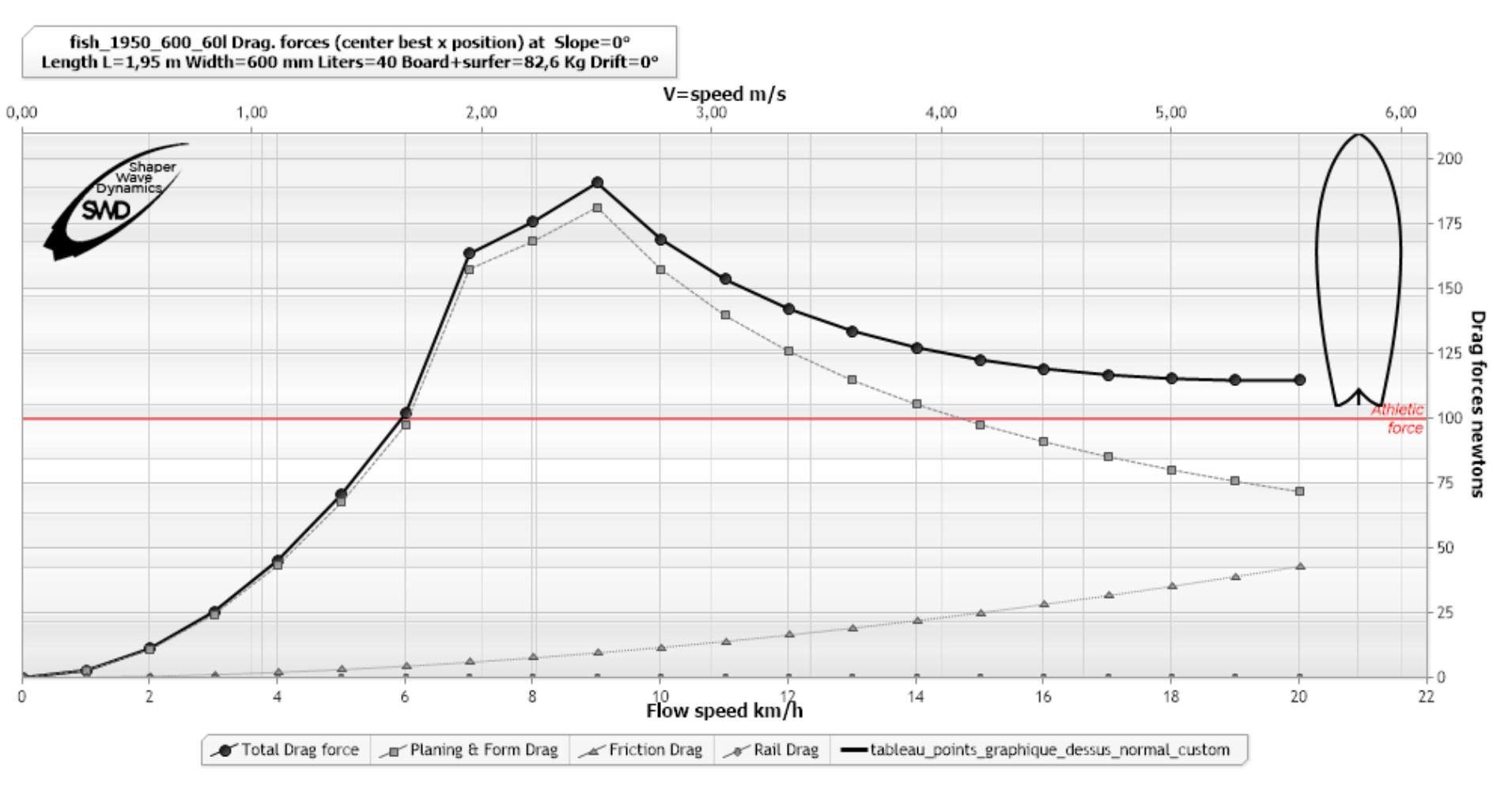
Let us now add to this graph a horizontal line marking the force of 100 N, which a surfer in good condition can reasonably provide:
(example Hydrodynamic drag analysis, software ShaperWaveDynamics)
If we note that the drag force at 3 km/h is 25N, the useful propulsive force at 3 km/h, for a surfer supplying 100 N to the oar will therefore be 100-30 = 70 newtons. it will only be 100-100=0N at 6 km/h and the surfer can never exceed 6 km/h when paddling on this board because its drag would then be greater than the propulsion and prevent any increase in speed. This graph therefore tells us that the surfer producing 100 N when paddling will reach a speed limit of 6 km/h, corresponding to the intersection of the drag curve and the 100 N red line. A given board therefore has a speed limit, for a surfer of given weight and strength. We are beginning to perceive the interest that the hydrodynamic drag curve can have for the shaper and the surfer.
- The placement condition: The question of placement can be summed up as: What distance does it take to go from zero to 3.1 m/s? The surfer answers this question empirically: By carrying out several attempts, he adjusts his position with each failure, until he succeeds in his take-off. But we would like to discover the potential theoretical levers for improving the take off. Physics textbooks give us a solution to the classic acceleration distance problem:
- Exposure duration strategy: being exposed for a maximum of time at a minimum of strength: This strategy allows take offs ahead of the peak, we will study it in detail later..
- Useful propulsive force strategy: be exposed for a minimum of time to maximum force: This strategy allows a take off very close to the peak, we will also study it later.
D = (Vc²-V0²)/(2*a) (ref: kane/sternheim Physique) With Vc peak speed, V0 initial speed, D= distance to travel to reach speed Vc, and a= acceleration in m/s².
This formula shows us that the placement distance, D, therefore decreases when the acceleration, a, increases.
The acceleration being by definition: a= (Vc-V0)/ dt, and the useful propulsive force, Fpu, being by definition Fpu= m*(Vc-V0)/ dt, we can reformulate by distributing on one side of equality, the variables that the surfer can control, and on the other the imposed parameters. Admitting V0=0, we get: Fpu*dt=m*Vc . For information, the physical term describing Fpu*dt, is the impulse. In other words, the useful propulsive force and the duration of exposure to this force, form the impulse. Impulse is the main factor in the take off. The Fpu*dt formulation highlights the strategies offered to the surfer to provide the same impulse:
These 2 strategies are extremes, the surfer has a possibility of proportioning between these 2 extremes. The analysis of these limits offers a vision of the range of use of a given board, for a given surfer, in a given wave. And that's what the surfer and the shaper wants to know before embarking on a purchase or a board design!
We might intuitively think that the strategy of force is reserved for muscular and powerful surfers, but this is not necessarily true, because of the various propellant sources available to the surfer. We have previously distinguished 3 sources of propulsion:
- rowing strength,
- the resultant force of gravity projected by the slope,,
- and the external traction forces of sail or jetski type...
We will exclude external forces from our questioning, to target the case of traditional surfing. We are therefore left with 2 sources, the oar and gravity.
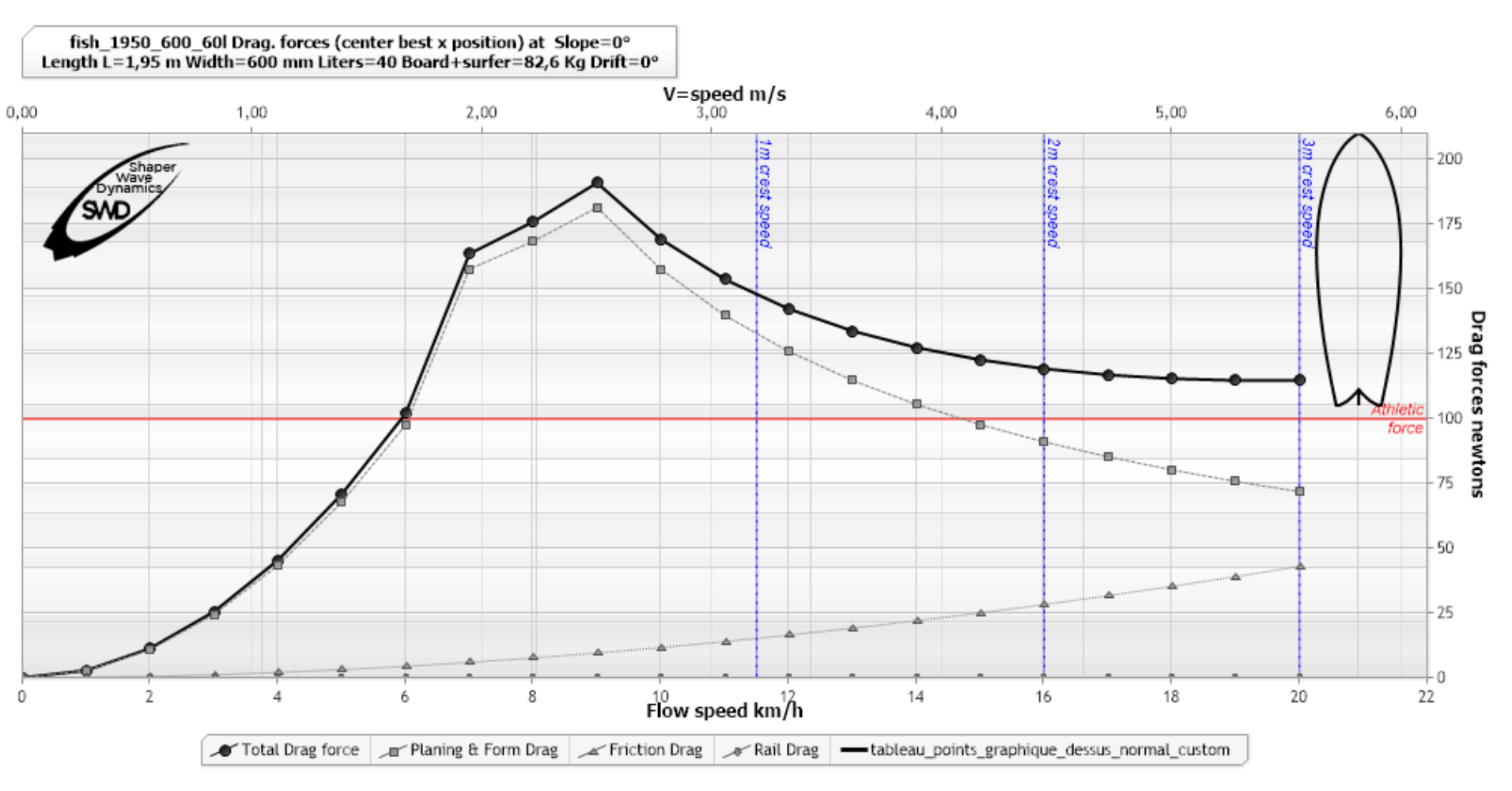
Let's add to our drag graph, 3 vertical markers, in blue, which respectively indicate the approximate crest speeds, of the 1, 2 and 3 meter wave, that the surfer must reach for his take off:
To reach the 11.5 km/h of the 1 meter wave, we see that it will be necessary to exceed a peak resistance of around 190 N. We see that our surfer producing a force of 100N when paddling, will be limited to 6 km/h. So the surfer needs another source of propulsion if he wants to take the 1 meter wave: gravity. Or more exactly, the reaction resulting from the wave in contact with the board.
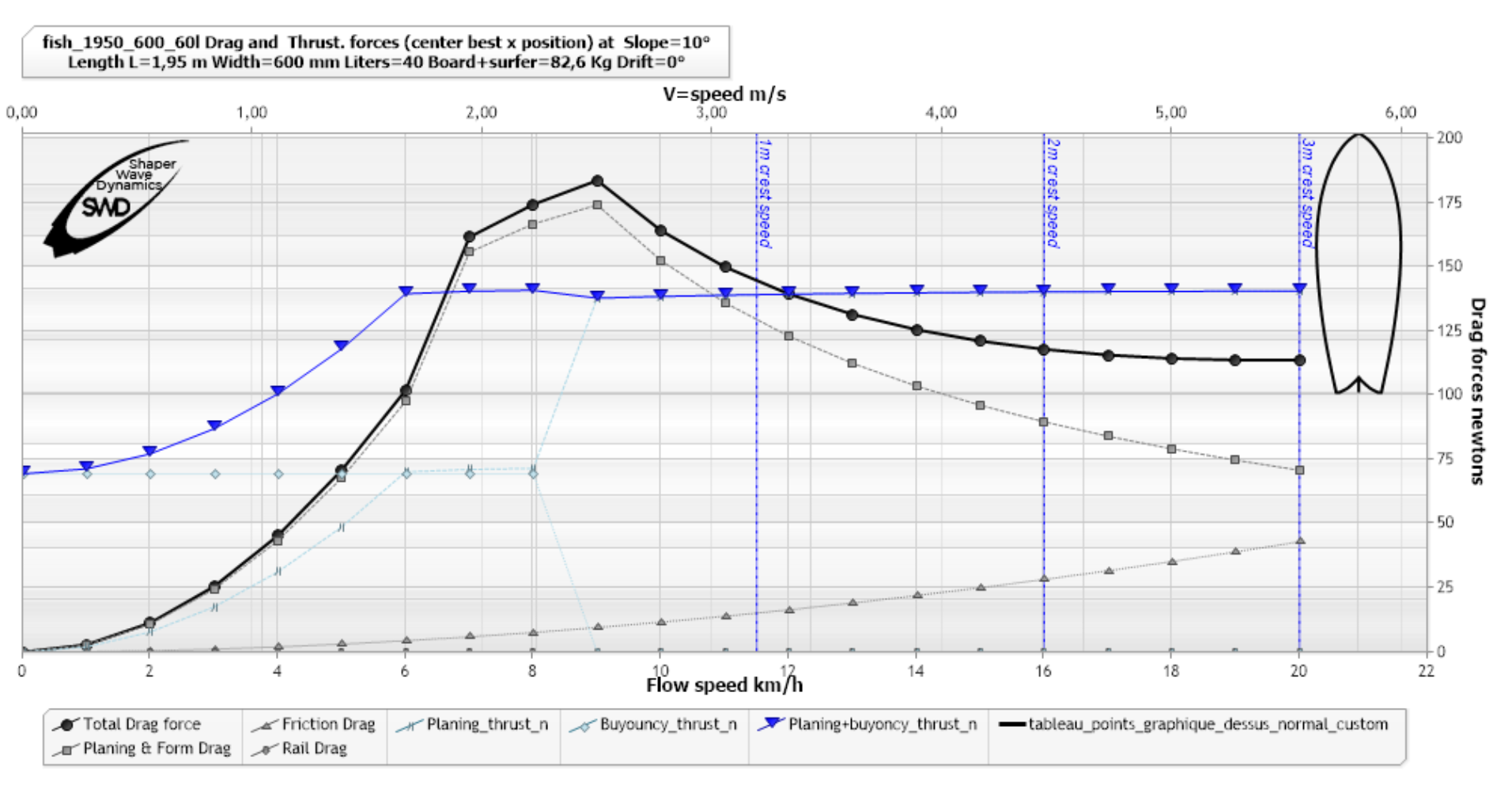
This gravitational thrust resulting from the lift (hydrostatic or hydrodynamic), increases according to the slope. Here are 2 graphs showing the thrust resulting from 10 and 15 degree slopes for the same board and the same surfer:
(blue triangles curve thrust) at 10°, software ShaperWaveDynamics)
The graph above shows us that a surfer exposed long enough to the 10 degree slope, will see his speed increase up to the limit of 6.5 km/h..
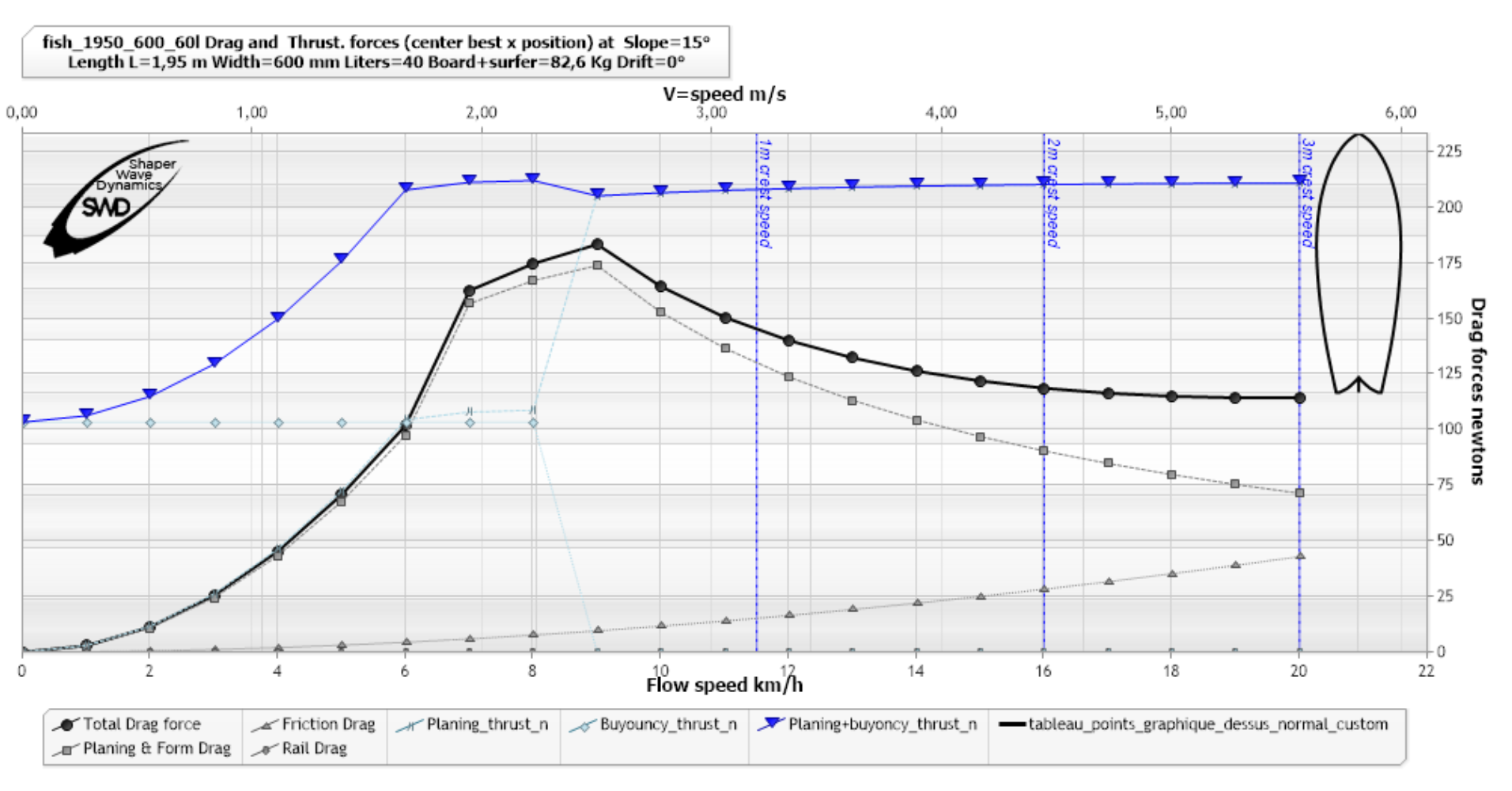
(blue triangles curve thrust) at 15 °, ShaperWaveDynamics)
The graph above shows us that a surfer in the slope of 15 degrees, at 6 km/h will be subjected to a gravitational Propulsive Force (buoyancy+planing) of 213 N and a drag force (drag) of 100 N. useful propulsive force will therefore be 213-100=113 N. The mass of the surfer+board being 82.6kg in this example, the acceleration at 6km/h of this surfer on this board, at 15 degrees of slope is therefore: F=m*a => 113/82.6=1.36 m/s²..
Here is the same graph with the acceleration:
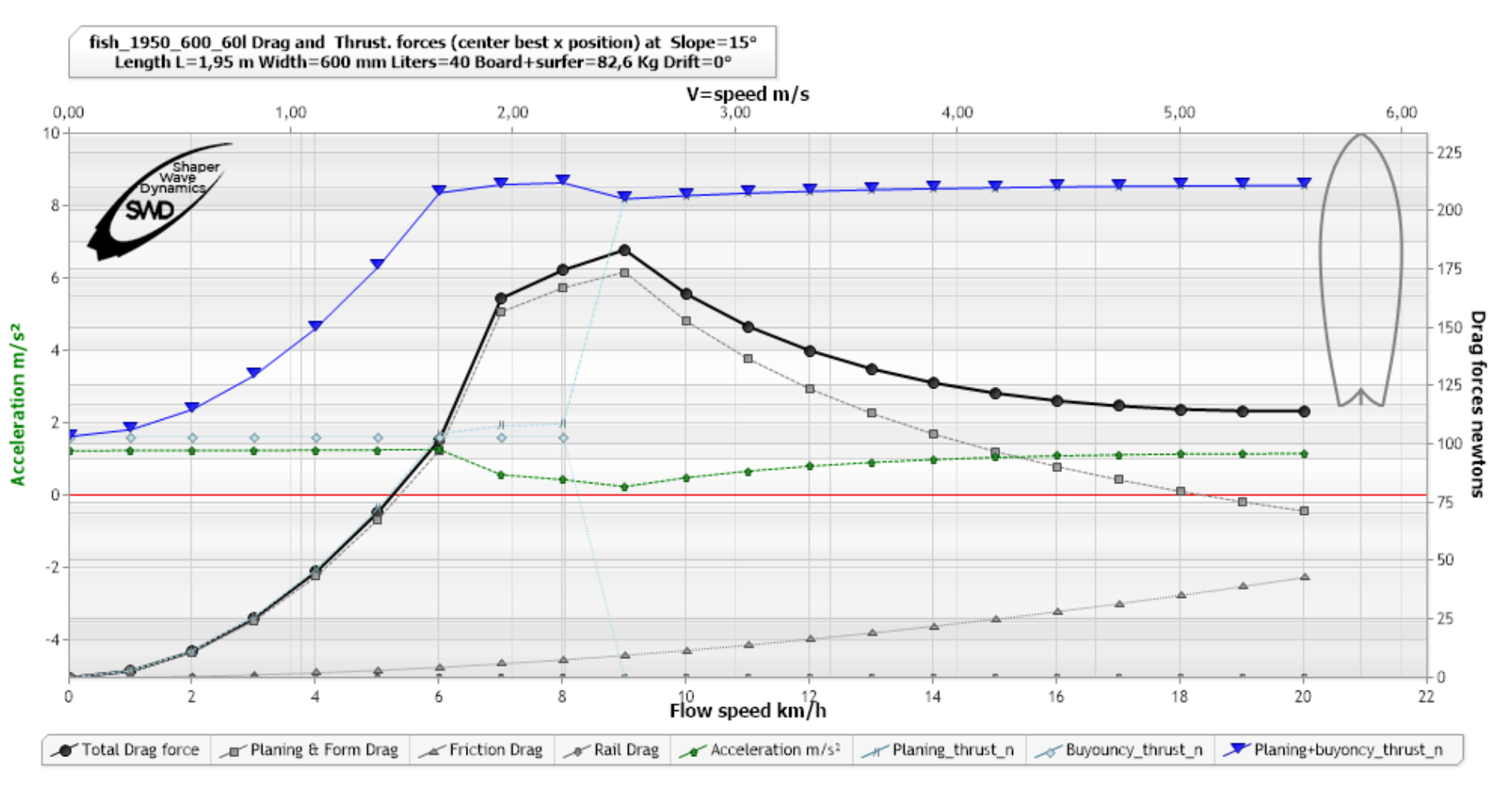
(Acceleration green curve dashed dots arrows) at 15 °, ShaperWaveDynamics)
and the acceleration for the 10 degree slope where we see a deceleration zone between 7 and 12 km/h:
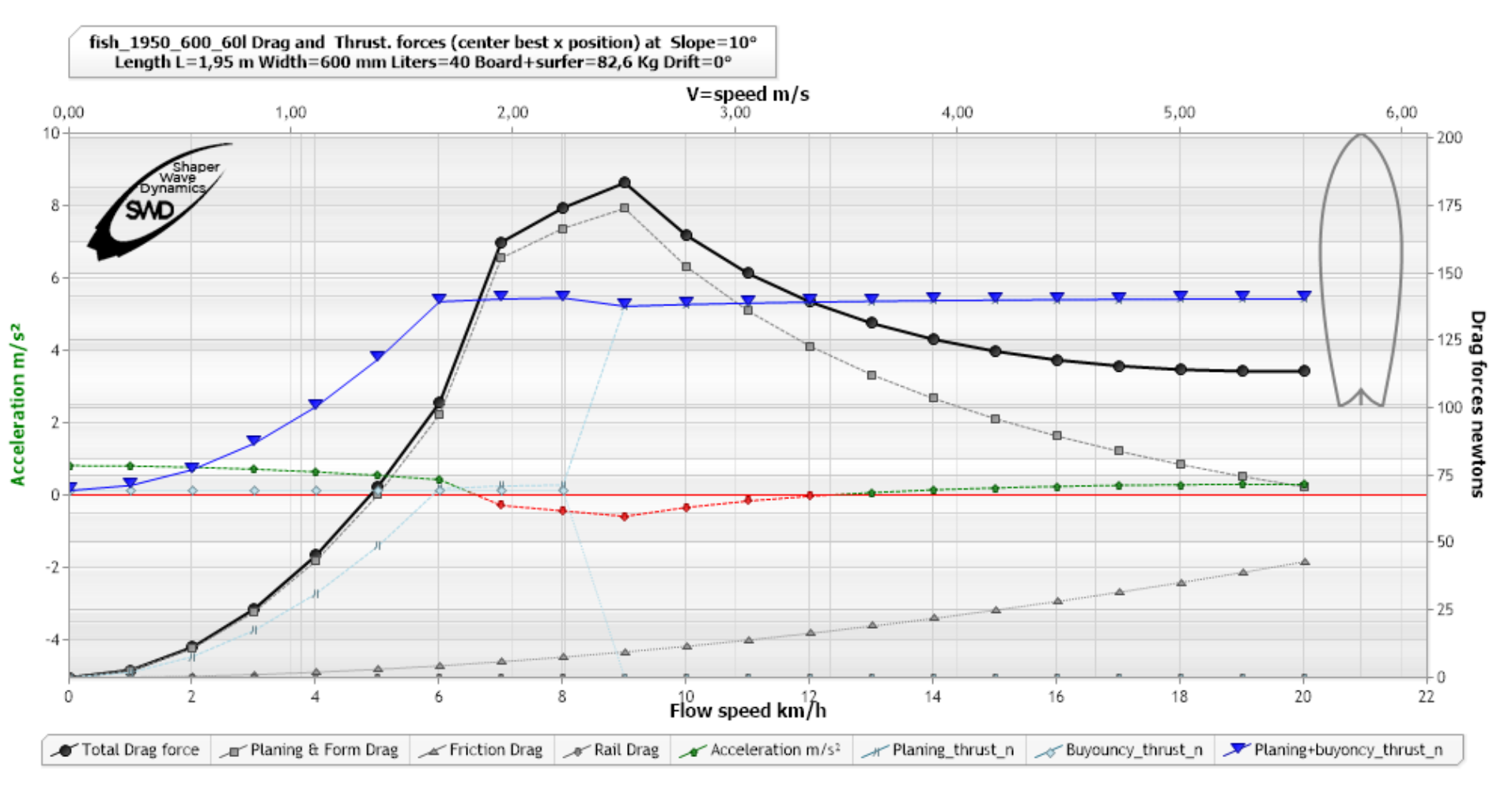
(Acceleration green curve dashed dots arrows) at 10 °, ShaperWaveDynamics)
In fact the surfer will be exposed to a given slope, for a given time only. Then the slope will change, moving from zero to 60 degrees. The surfer will therefore be exposed, for a moment dT, to 1 degree, then to 2 degrees, then to 3 degrees, then ... OK I stop. In reality this change is continuous and progressive, but we can estimate that if we know the duration of the slope variation, dT, for 1 degree, and the acceleration at this degree of slope, we can obtain the speed variation dV, produced at every degree:
dV=a*dT
This duration dT we have in fact already defined it above when we linked the slope to the period: We know that our slope evolves from 0 to 60 degrees in 1/4 of a period. (To be more precise we should use a variation based on the sine of the angle, but let's stay in a linear approximation, which will be more than enough between 0 and 60 degrees.) The duration of variation of 1 degree is therefore:
dT=period/4/60=period/ 240.
Let's take a surfer + board of mass 82.6 kg, positioned at the slope 0 degrees slightly off the peak, of a wave of period 12 seconds breaking on a bottom of 1 meter (we estimate that the wave height and the depth at the peak are equivalent), at a speed of 3.1 m/s.


(Interface details Analysis take off, of the software ShaperWaveDynamics)
If he does not move, the surfer will see the slope evolve from zero to 60 degrees in 3 seconds.
- Note: We can thus evaluate how far the 60° slope (breaking) is when we perceive a certain angle of slope at our position, using the peak speed: for example Distance of the 60° slope when the surfer is at the slope 0°=3*3.1=9.3 meters. We intuitively use this type of slope estimation when rowing, and guess without looking back, if the peak is closer or less close, depending on the slope felt..
the lapse of time, dT, to increase by 1°, the slope of our wave of 12 seconds of period, is therefore: dT=period/ 240=0.05 seconds
Let's observe the evolution of the surfer's speed at each degree of slope: V0°, V1°,V2°,V3°,V4°....:
Starting at zero speed, at 0° degree, the surfer will not receive any gravitational propulsive force, and he will therefore have to row to generate acceleration. Assuming that it produces a propulsive force of 100 N when rowing, and that when stopped it encounters no resistance to progress, its acceleration will then be F=m*a => a=100/82.6=1.21 m/s². We can say that its speed will evolve from V0° to V1° during an interval dT=0.05s, following V1°=V0°+(1.21*0.05)=0.06 m/sec.
The surfer is now on a 1° slope, with non-zero speed...
A small finesse, which will appeal to surfers sensitive to the temporal distortion felt during surfing, must now be added to our calculation: The variation time per degree, dT, is modified by the speed of the surfer: Indeed, if the surfer moves at the same speed as the wave, he will not perceive a variation in the slope, because he accompanies it. This is also where the sensation of surfing resides: the surfer follows a "timeless" event in a purely geometric reference frame, the reference of which is the slope. A wave that opens is a wave where the surfer perceives a constant slope that he can follow. This subjective geometric aspect of surfing is more extensively developed on the page geometric thinking.
If the surfer is moving, we must therefore take into account the "stretching" of the slope variation time, dT, produced by the "accompanying" speed of the wave. We therefore introduce an accompanying factor, aV, which tends to increase dT when the surfer's speed, Vs, increases. aV tends to infinity when Vs reaches the wave speed, and tends to 1 when Vs = 0: We therefore define the Accompaniment Factor aV=Vc / (Vc - Vs), in the limit Vs<Vc and must reformulate our interval: dT = period/ 240 * aV
We therefore go from a speed at a slope n°, to a speed at the following slope n°+1 according to the formula::
Vn°=Vn°-1+(an°*(period/ 240) * (Vc / (Vc - Vn°-1))
with an°, the acceleration calculated at the following slope n°: Fpun°=m*an° => an°= Fpun-1°/mass_kg , with Fpun° the useful propulsive force at slope n°-1 depending speed Vn°-11
When Vn° reaches peak speed we have solved for the minimum take off slope for the given surfer and board::
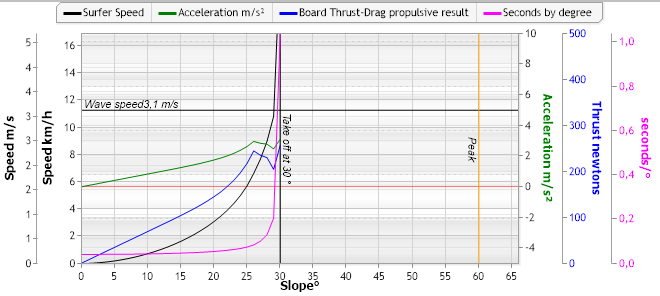
(Acceleration ramp depending on the slope),ShaperWaveDynamics)
This graph shows the evolution of useful propulsive forces, acceleration, speed and stretching of slope duration per second, for a board and a given surfer weight. The surfer will reach the Wave speed of 1 meter (3.1ms), when the slope is 30 degrees. By knowing the evolution of speeds, we can position the surfer at each point of the acceleration ramp and determine the distance covered. Here is a diagram indicating for a given surfer, on a given board, in a given wave, considering that the surfer realizes the take off when he reaches the wave speed::
- the distance traveled to join the wave starting from a slope and zero speed
- the time to join the wave starting from a slope and zero speed.
- The remaining distance before breaking, when the surfer is in a take off position
- The remaining distance and the time before breaking, when the surfer is in a take off position
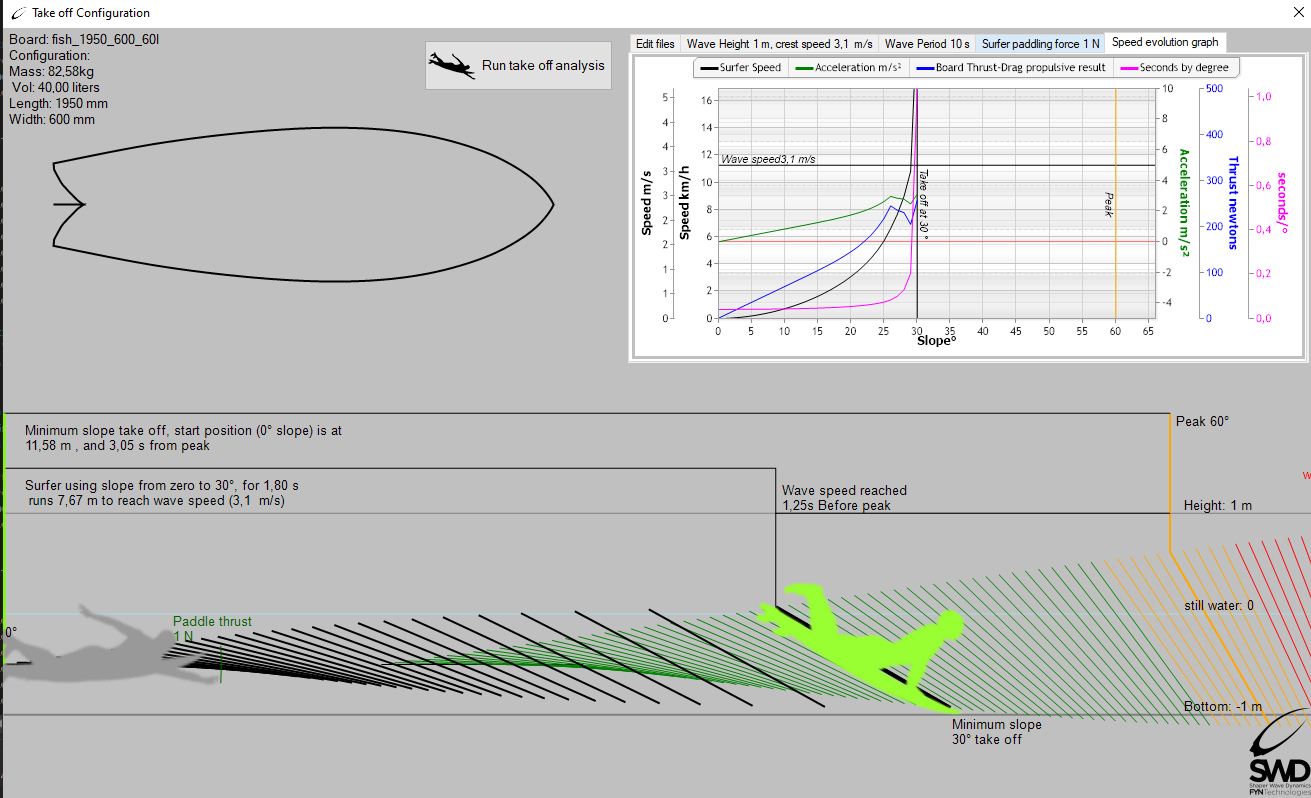
( take off, ShaperWaveDynamics)
The placement is therefore described by a distance, but it also conditions the slope at which the take off can be made with a given board. This analysis with a take off on minimum slope, describes the strategy of maximum exposure to the slope with the minimum effort. It is the one that gives the surfer the possibility of getting up the earliest. It is by testing various shape hypotheses, with this software tool (Take off analysis, ShaperWaveDynamics software), that the shaper and the surfer will be able to assess whether their board project is better than another by comparing the minimum take off angles. off, before embarking on the realization of the board.
Let's see the strategy with maximum effort and minimum exposure duration::
We previously calculated the minimum take-off slope, by initializing our calculation with a surfer placed on the 0° slope. We have seen that the propelling force must be positive to start moving..
The surfer can remain seated on his board, without rowing, so as to create maximum resistance to the advancement, neutralizing the gravitational propulsive force, and thus letting the slope increase, without being propelled or moved.
 The surfer can thus wait, and choose to lie down in the minimum drag position,
The surfer can thus wait, and choose to lie down in the minimum drag position,
 at a steeper slope to begin its acceleration ramp.
at a steeper slope to begin its acceleration ramp.
We can evaluate the maximum starting slope, which generates an acceleration ramp allowing to reach the wave speed before the breaking occurs. To do this, simply initialize the calculation of the acceleration ramp, no longer with a starting slope of 0°, but with higher values, until you obtain the starting slope which produces a catch-up of the wave a 60° (moment of peak). We will thus have described the condition of "no padlle take off", or late take off, corresponding to the strategy of maximum force and minimum impulse time::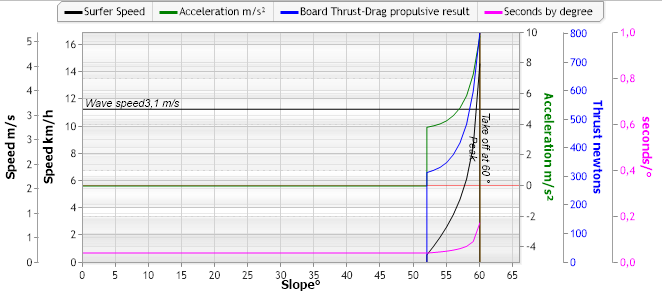
(Acceleration ramp starting at 55° ShaperWaveDynamics)
We see in the graph above an acceleration ramp generating an increase in speed starting from 0 m/s at 52 degrees of slope, and reaching the speed of 3.1 m/s at 60°. Note that the propulsive forces (blue curve) start at 320N at 52° to rise to around 700N at 60° at the time of the take off. It's a force strategy, even if the surfer does not row!!!
(Search for maximum take off slope ShaperWaveDynamics)
Conclusion:
A board of given volume and shape, produces a hydrodynamic drag, which varies according to the speed and the weight of the surfer. It is possible to deduce from the drag curve, as a function of the speed, the acceleration capacities of this board and to determine, for a wave of given period and size, the minimum slope of take off, and the slope of maximum departure for the surfer and his board, in this wave.
The calculation hypothesis used here does not seek to precisely define values which in reality depend on more factors than those chosen. Our hypothesis admits, for example, a breaking angle of 60 degrees, but this angle varies according to the conditions, for example wind: an offshore, will hold back the breaking and push it back a few degrees. But taking a given hypothesis, and using it to compare various boards, is the most effective method for benchmarking, as it provides a stable and objective viewpoint that the shaper and surfer can refer to to relate their experience to a stable theoretical basis..
We see and understand by this theoretical approach, that the strategy of force is not reserved for powerful surfers, it is even quite the opposite. This is counter-intuitive for the uninitiated to the notion of impulse, but becomes intuitive and clearer for the insider, who will be able to integrate the theory into his investment strategy on his spot, depending on his board, the study of hydrodynamics sharpens our instincts!
We see the interest of a tool for calculating the performance, even if it remains theoretical, of a given board, which gives the shaper and the surfer a prediction of the board's ability to take off. But the qualities of a board, in terms of dynamics, do not only reside in the take off skills, it will also be necessary to evaluate the skills of the board in terms of stability and maneuverability, we will see this in the chapter surf maneuverability