The trajectory, of the surfer in balance, is a vector which can be modified in speed and direction. Maneuverability is the ability to modify this trajectory vector, by imbalance and return to equilibrium:
- speed variation (Acceleration/Braking)
- variation of direction (Radius of curve)
In surfing, 2 types of surfer movements, which alter the balance of lift forces, produce these trajectory changes::
Front-to-back displacements of the center of gravity= speed variation..
- Accelerate = lean forward: When a runner wants to accelerate, the chest and shoulders move forward and move the center of gravity forward, this movement is instinctive and strongly anchored in us as the will to accelerate
- Braking = leaning backwards: conversely when this runner decides to stop he pulls back his shoulders to anticipate the increase in support under his feet, which must remain in front of his center of gravity to avoid tipping.
- Stay at the same speed = maintain the center of gravity between the two feet.
Lateral displacement of the center of gravity=direction variation.
- Changing direction = The center of gravity is naturally positioned towards the inside of the turn to compensate for centrifugal force. It is surprising to see how our mind is capable of flight, just watch a child run imitating an airplane, he bends his winged arms towards the inside of the turn as if to lean on the air, as does the bird, plane or dolphin with its pectoral fins in a sharp turn.
These rules that play with balance are a natural logic for our body..
An "intuitive" board, technically corresponds to the ease of turning in the 3 axes Pitch Roll and Yaw (Yaw/Pitch/Roll) following our natural movements.
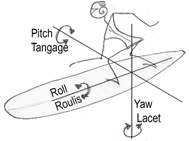Yaw/Pitch/Roll
- The pitch/pitch generates acceleration or braking by modifying the planing angle according to the position of the surfer. The distribution of the surface of the outline on the nose or the tail, the presence or not of a flat zone of rocker, strongly impacts this maneuver.
- The rotation of Roll/Roll produces the turn, by laterally projecting a component of the planing lift (like the plane mimicked by the child), and immerses the rail by printing the curve of the rocker in the wave. The shape of the outline determines the immersion of the rail and the dynamic distribution of forces around the surfer's center of gravity. Maneuverability increases with the ease of varying the roll angle.
- The yaw/yaw does not modify the trajectory, only the angle between the board axis and the direction of the trajectory. This is the drift angle of the board, it is possible to yaw 360 degrees without changing the trajectory.(see surf drift angle)
To understand the maneuverability of a board we must distinguish between the maneuvering lever and the maneuver itself. :
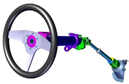When we turn the steering wheel of a car, it changes course with varying degrees of efficiency. The force you apply to turn the steering wheel is not directly the one that modifies the trajectory of the car, if the steering column is broken you will have a maneuvering lever (steering wheel) very easy to operate, but no modification of trajectory !
Reminder: In mechanics, a lever effort connected to an axis is a "moment", it is expressed in newton x meters. 1 N.m is a force of 1 newton applied perpendicularly to a 1 meter lever linked to the axis. When our toes submerge the rail, we apply a rolling moment equal to: (force pressing our toes) x (distance from the roll axis). If no opposing force balances the effort, we tip over and lose control. Fortunately, when we apply moment with our toes, a counter moment is produced by the hydrodynamic and hydrostatic forces and stabilizes the roll maneuver. A moment and its opposite moment define the equilibrium called torque. The rotational acceleration is zero when the moments are balanced in a couple..
When I turn my steering wheel slightly, I apply a moment which causes it to rotate, but I feel an opposite moment to the force I apply, otherwise it would start to turn faster and faster without any additional effort and I should quickly reverse my effort so as not to go into the background. Modern cars are equipped with power steering which could totally remove any effort on the steering wheel. But the manufacturer leaves a resisting force, so that the driver can intuitively adjust the rotation, and when you release the steering wheel it comes back to the straight position, it's intuitive ergonomics. This resistance of the system to the change of state provides stability, if the action generates a change of state which self-amplifies the system becomes uncontrollable and unstable. This "systemic" vision tells us about the character and functional limits of the board-surfer-wave system..
In surfing, the steering wheel is the lateral displacement of the center of support, and the accelerator pedal is the longitudinal displacement of this same center of support. A wide board can allow a strong lateral movement without causing a lot of roll, for example, The final efficiency results from variations in roll and pitch..
When we want to turn by moving our center of gravity laterally, we appreciate that the board resists a little (but not too much) under our toe in order to be able to control the maneuver, and when we release this pressure we appreciate that the board returns to its angle initial roll without having to play too much heel. To achieve this intuitive ergonomic control, without losing balance, the board must be "self stable"..
Imbalance and return to equilibrium:
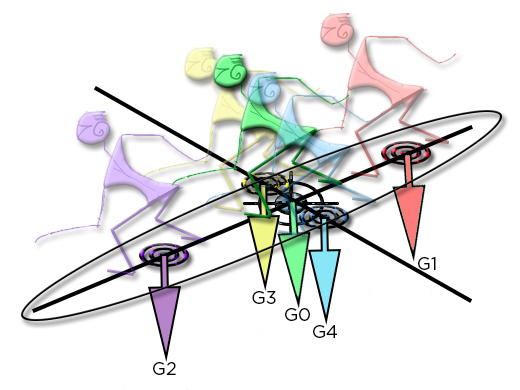
If I am in balance at point G0, it is because my fulcrum is at the center of lift. If I move my support from G0 to G3, I must feel a "counterforce", generated by the lift, which increases and limits the roll rotation, otherwise it is an unstable tilt and a fall. Same thing if I move from G0 to G2, I generate a pitching moment which must be counterbalanced by an inverse moment generated by the lift. The stronger the moment of resistance, the more stable my board. If the hydrodynamic "counter-moment" becomes lower than the moment generated by the support of my center of gravity, the forces no longer restore balance, my board becomes unstable. So let's take a closer look at the roll and pitch lever stability of our board..
The three axes of yaw, pitch and roll (yaw, pitch, roll) intersect at the point of application of the surfer's center of gravity, which we call the center of support.
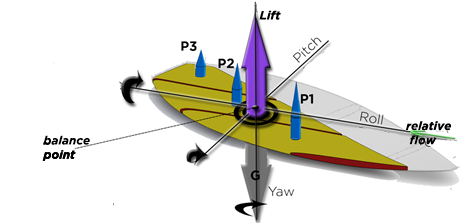
For example, we have cut a board into 3 slices parallel to the relative flow, 3 elements facilitating the calculations. We can estimate the longitudinal and lateral position of the balance point based on the lifts of these elements, isolating the board along the roll and pitch axes: :
- Pitch axis view :
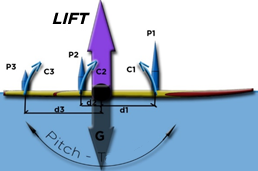
Positions of equilibrium of the pitching moments resulting from the elementary lifts
- Roll axis view:
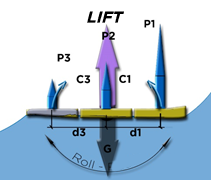
Positions of equilibrium of the rolling moments resulting from the elementary lifts
We can write the equilibrium condition in the Roll, and Pitch planes :
C1 + C2 + C3 = 0 with torque : C (N.m) = d(m) x P(N)
This relation defines the position of the equilibrium point. The center of support of the surfer is the lever controlling the roll and the pitch. If the fulcrum moves, the balance is broken and the angle will change, this modifies the lift forces depending on the shape of the board and the speed, and recreate a balance at another angle, or not . We can assess the character of a board based on the relationship angle<=>displacement: the greater the displacement per degree of variation, the more stable the board is on this axis. We can thus evaluate the amplitude of possible displacement, laterally and longitudinally, for a surfer of given weight on a given board.
To assess the maneuverability of a board in a given situation, we must therefore show::
- how the variation in the surfer's lateral position varies the roll, but also how this impacts the variation in direction. the relation between the roll and the curvature of trajectory results from the projections of lift, it is studied in detail in the chapter Surf turns.
- how the variation in the longitudinal position of the surfer varies the angle of attack, but also how this impacts the variation in speed. The relation between the pitch and the acceleration is the relation incidence and hydrodynamic drag, it is studied in detail in the chapter surf hydrodynamics drag.
By drawing a map of the positions on a given board, at given speed, surfer weight and wave slope, and displaying, according to a color code, the roll angles, the trajectory curve radii and the drag forces, which define the ability to change speed and the angles of incidence that are the cause of these hydrodynamic phenomena, we obtain a "HydroScan" objectively arguing the maneuverability of a board, bare without fins. (We will explore the impact of fins separately in the chapter dealing with aileron dynamics).
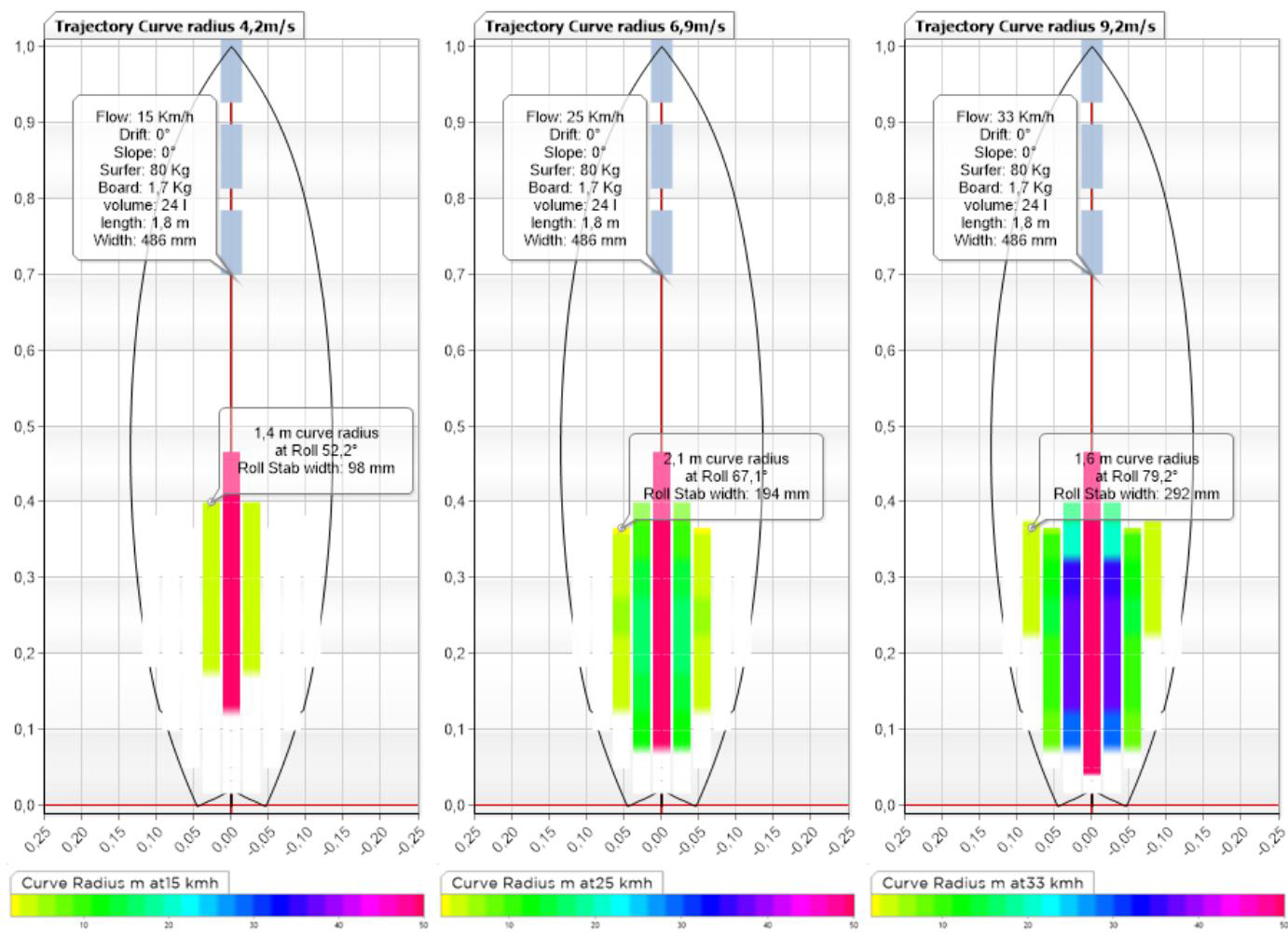
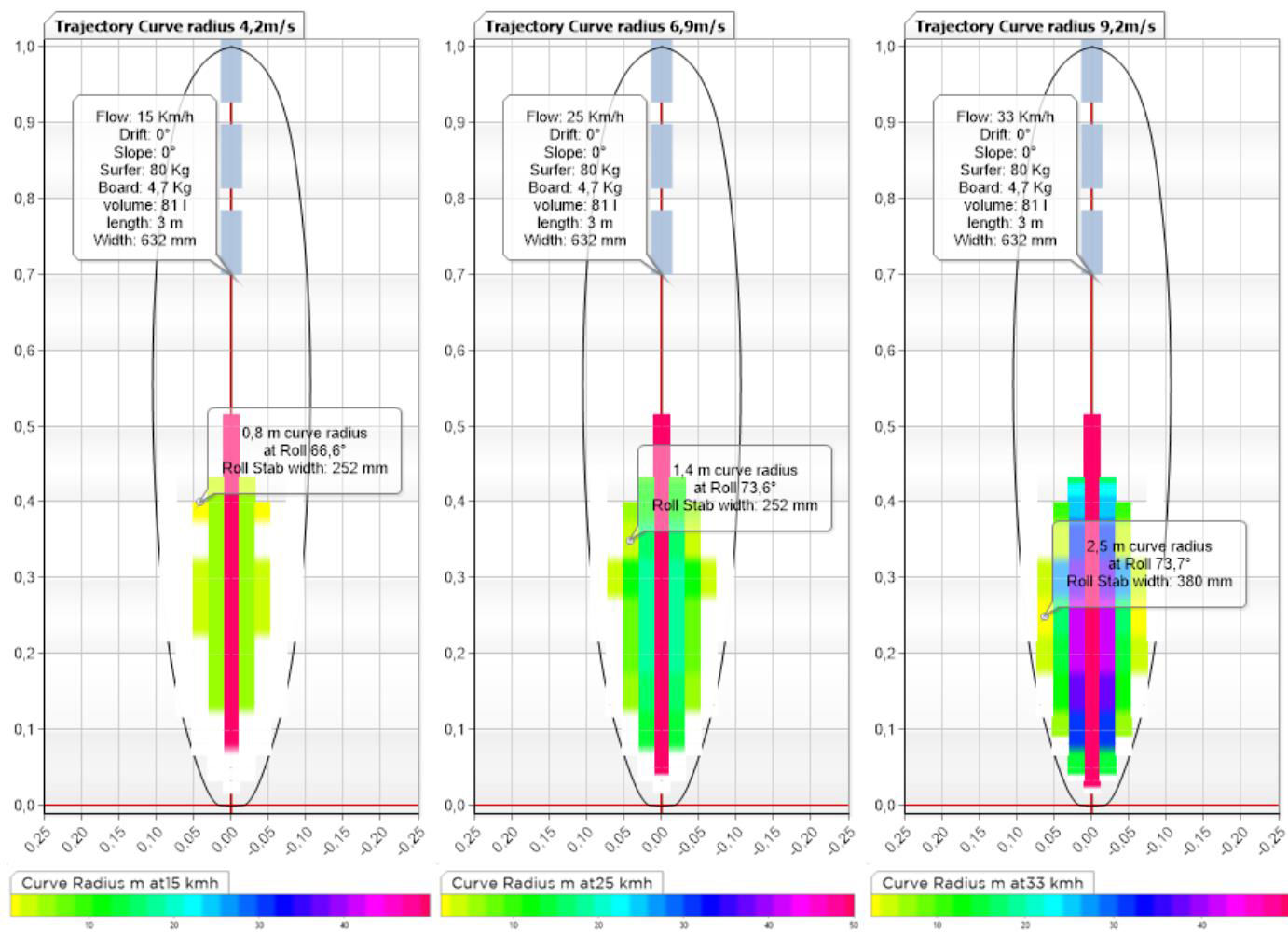
HydroScan maneuverability curve trajectory, shortboard software ShaperWaveDynamics:
We see above, the possible balance positions (apart from these positions there is loading, loss of balance or loss of lift) of the same board at 3 different speeds. It is easy to see that the maneuverability in terms of turns is easier at low speed (first image on the left) because you can reach a very tight trajectory radius of 1.4 m (very radical!) by moving the support very little lateral, and with a roll of about 47 degrees, but beware the width of the "Roll stab width" (colored surface) is very narrow (98mm), this means that the board is really unstable at this speed. If we look at the image on the right, at higher speed we see that we gain in stable zone width (292mm), and that we can reach a high roll angle (77 degrees) producing a radius of 1.6 M.
The link between stability and maneuverability as a function of speed becomes evident in this presentation, the surfer experiences instability at low speed, and the difficulty of turning when speed increases involving carve support and engaged roll angles.
What is particularly interesting to note for the surfer and the shaper is the width of the stable zone that we will compare with another board to know if we gain or lose stability from one project to another..
Now let's take the same surfer, in the same speed conditions but on a longboard:
HydroScan of a longboard made with the software ShaperWaveDynamics:
the width of the stable zone is larger, and shows the gain in stability, but we also see the radius of the curve at high speed which becomes larger We can also compare the variations of planing angles and the variations of corresponding drag forces on these two boards through the following Hydroscans...
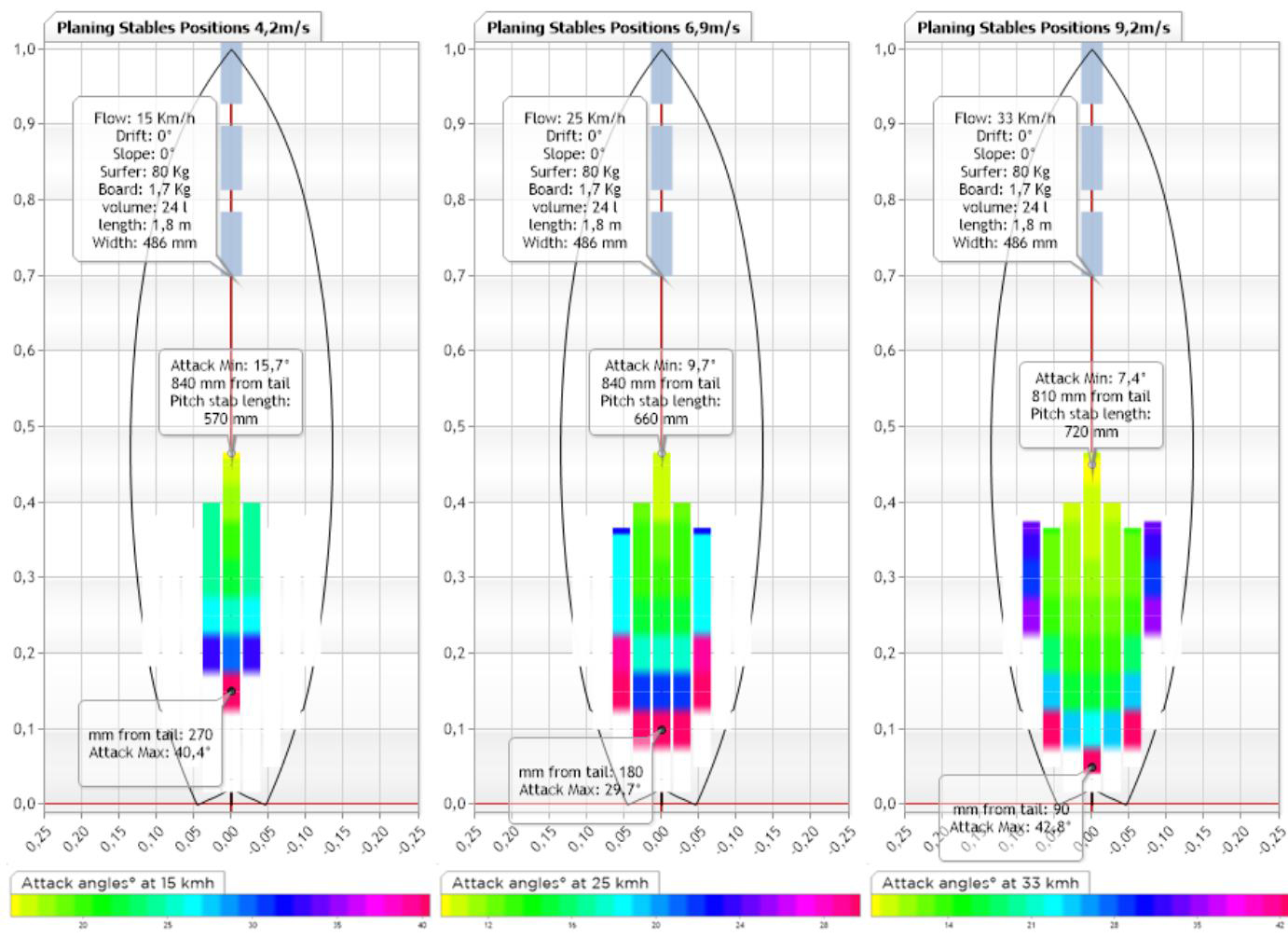
performance angles attack short board
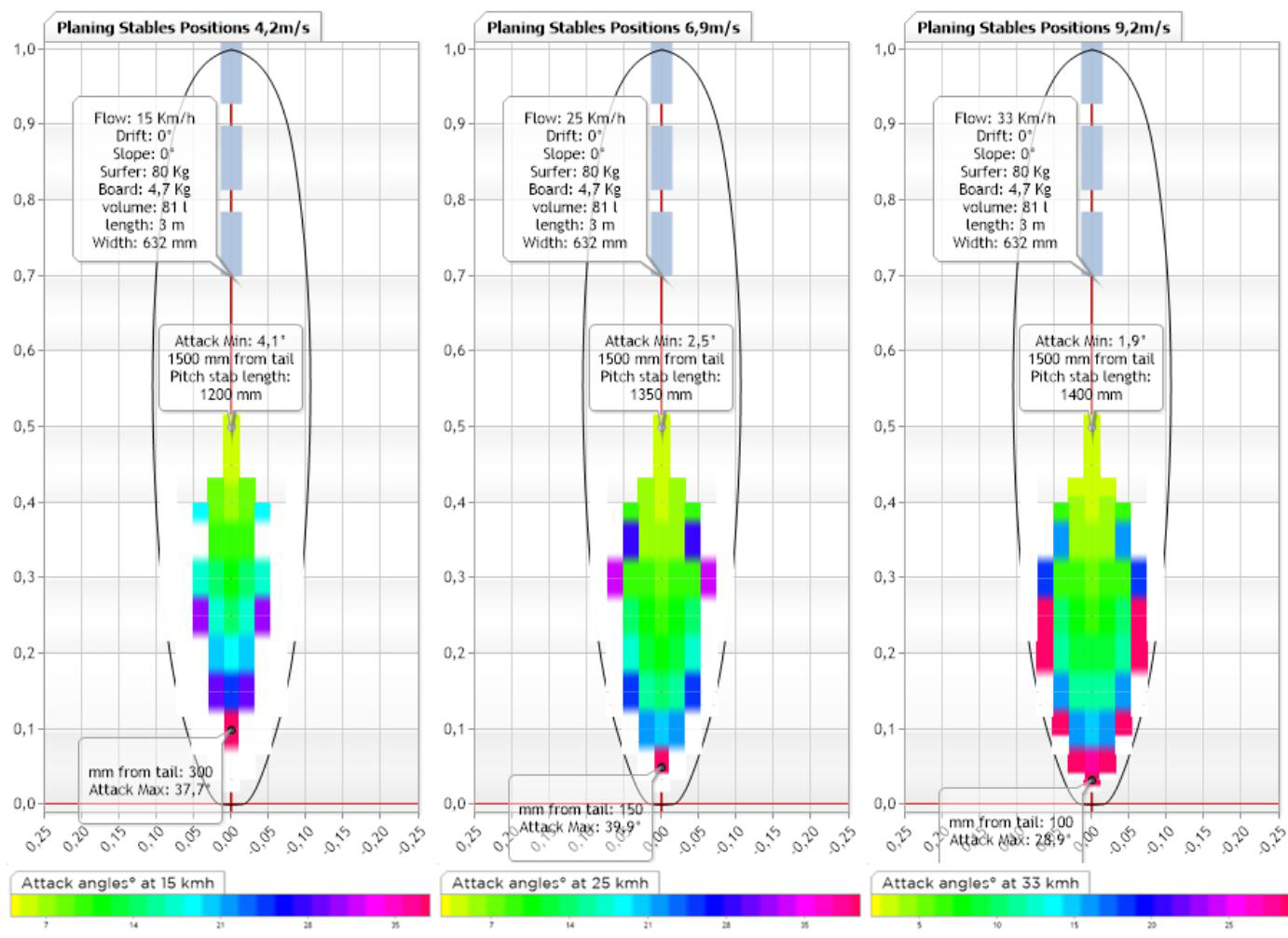
performance angles attack longboard
By observing the HydroScans of the planing angles, we notice the length of the stable pitch zone (pitch stab length) which goes from 720 mm for the shortboard at 33 km/h, to 1400 mm for the longboard at 33 km/h. it will therefore take very little movement on the shortboard to vary the incidence, and therefore the variation in speed of the board, while you can walk more on the longboard without modifying the speed too much...
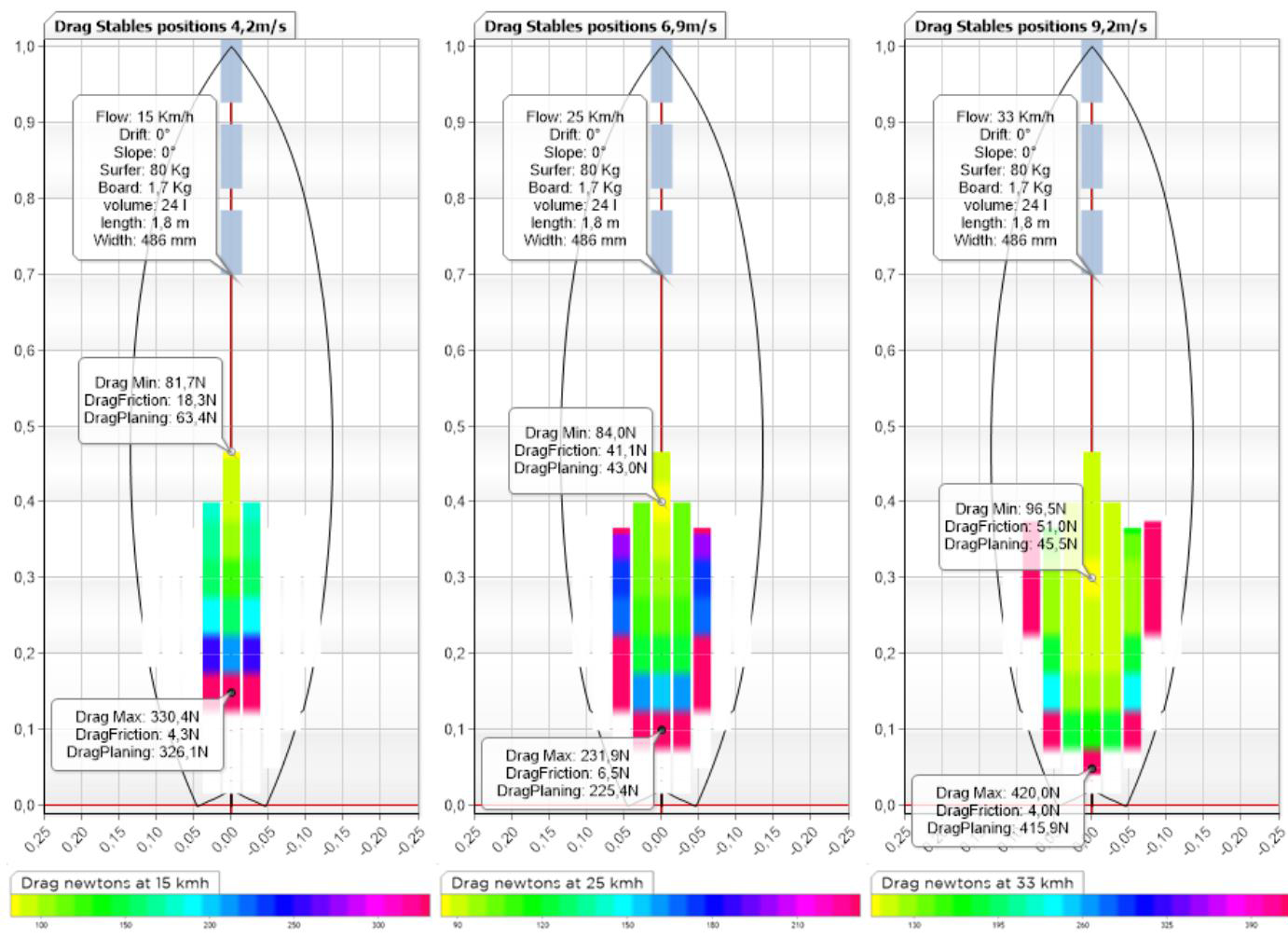
drag forces performance surfing shortboard
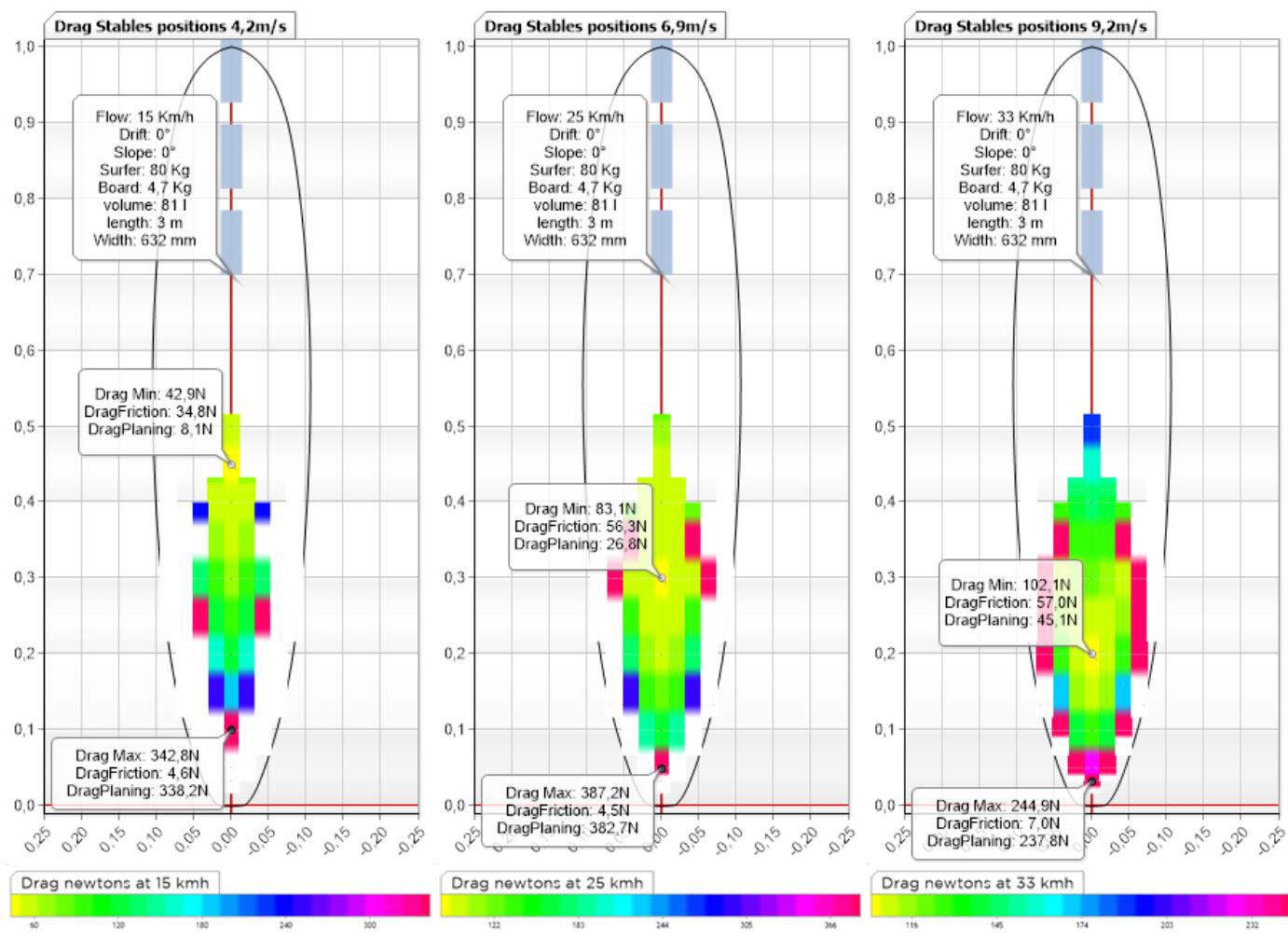
drag performance on a longboard
If we want to deepen our mastery of the hydrodynamics of surfing, it is important to separate the drag of friction and the drag of planing (shape), we can thus see that the longboard generates little drag of shape at low speed because it does not need much incidence to carry the surfer, so it generates less overall drag than the shortboard at low speeds, but as the speed increases the frictional drag increases more on the longboard, and one finds the minimum drag position of the longboard further back at high speed than at low speed to limit the friction surface by looking for the planing angle...
With this type of hydroscan, the surfer and the shaper are able to objectively argue the advantages and weaknesses of the various surfboard models they wish to study. The shaper and the surfer can edit these comparisons for various surfer weights, board sizes... in order to choose and select the board project best suited to their vision of surfing.
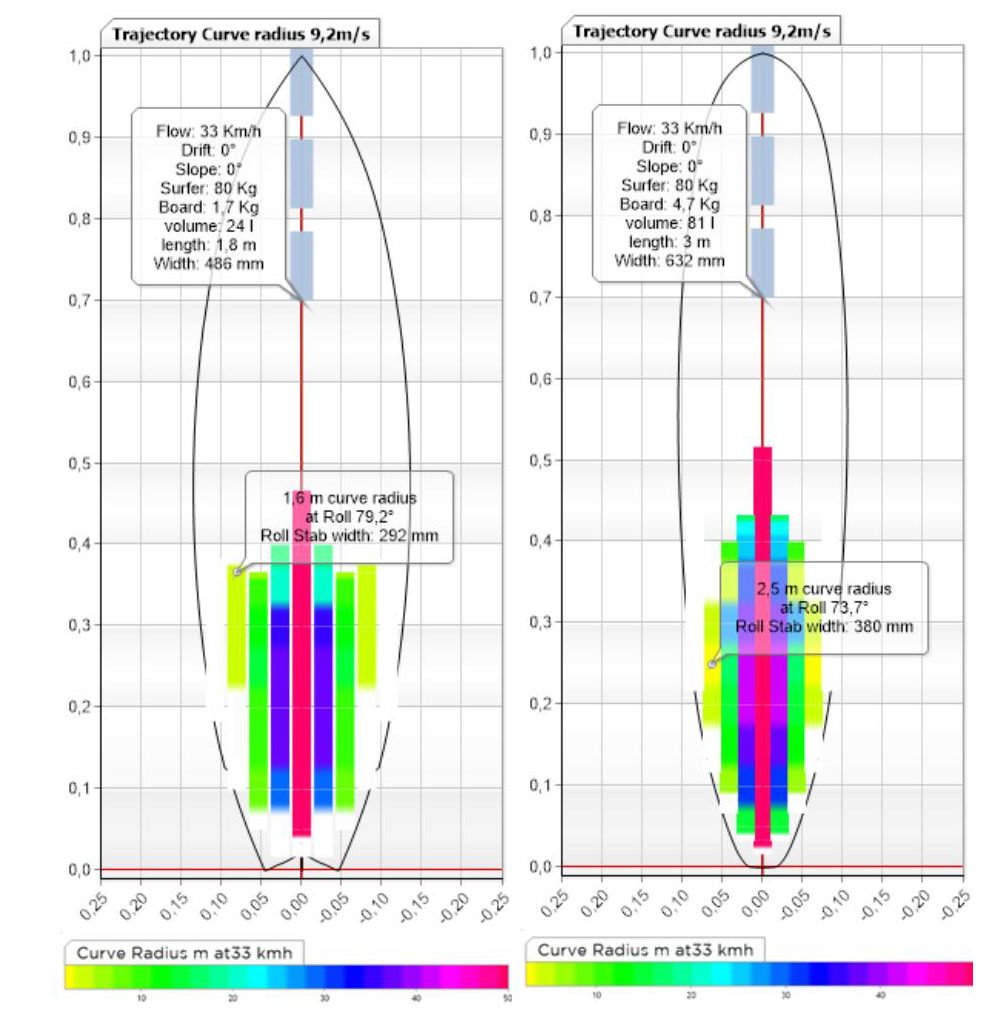
"Hydroscans" comparing the maneuverability performance of a short board and a longboard made with the software ShaperWaveDynamics